CONCEITO/EXPLICAÇÕES
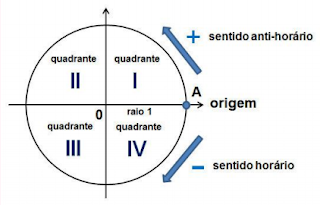
A circunferência
trigonométrica ou ciclo trigonométrico é de extrema importância para o estudo
da Trigonometria, pois é baseado nela que todos os teoremas são deduzidos.
Trata-se de uma circunferência com centro na origem (O) do sistema de eixos
coordenados e de raio 1.
Os eixos dividem a
circunferência em quatro partes congruentes, denominadas quadrantes.
Convenciona-se que, o sentido anti-horário é o sentido positivo na
circunferência trigonométrica, a partir de um ponto fixo (A), como é mostrado
na figura abaixo:
Ø A extremidade de um
arco , localizado no primeiro quadrante (I), satisfaz à seguinte desigualdade:
0º < α < 90º
Ø A extremidade de um
arco , localizado no segundo quadrante (II), satisfaz à seguinte desigualdade:
90º < α < 180º
Ø A extremidade de um
arco , localizado no terceiro quadrante (III), satisfaz à seguinte
desigualdade:
180º < α < 270º
Ø A extremidade de um
arco , localizado no quarto quadrante (IV), satisfaz à seguinte desigualdade:
270º < α < 360º
Esquematizando,
temos:
Quando dois arcos
diferentes terminam na mesma posição da circunferência trigonométrica, dizemos
que esses arcos são arcos côngruos.
Dizemos que 3/p rad 7p/3 rad são arcos côngruos, pois suas extremidades
coincidem na circunferência trigonométrica. (420º:360º deixa resto 60º ).
Assim,
podemos ver que qualquer arco α é côngruo com
outros infinitos arcos definidos pela soma de α
com múltiplos de 2p,
ou seja, se estamos sobre o arco β e andamos mais 2p
sobre a circunferência voltamos para a mesma posição e assim sucessivamente.
Desse modo, podemos escrever que qualquer arco côngruo de α
é da forma:
AB = α + 2kp,
com α ∈ Z
Expressão
usada para todos os arcos côngruos a α.
Ø K
é o número de voltas, também indica o sentido (negativo ou positivo) do giro.
Ø α
é a primeira (menor) determinação não negativa ou até mesmo positiva de um
arco.
Arcos de uma Circunferência
Ø Se
um ponto móvel em uma circunferência partir de A e parar em M, ele descreve um
arco AM. O ponto A é a origem do arco e M é a extremidade do arco.
Ø Quando
escolhemos um dos sentidos de percurso, o arco é denominado arco
orientado e
simplesmente pode ser denotado por AB se o sentido de percurso for de A para B
e BA quando o sentido de percurso for de B para A.
Ø Quando
não consideramos a orientação dos arcos formados por dois pontos A e B sobre
uma circunferência, temos dois arcos não orientados sendo A e B as suas
extremidades.
Medida
de um arco
Ø
A medida de um arco de
circunferência é feita por comparação com um outro arco da mesma circunferência
tomado como a unidade de arco. Se u for um arco de
comprimento unitário (igual a 1), a medida do arco AB, é o número de vezes que
o arco u cabe no arco AB.
Ø
Na
figura abaixo pode- se observar que, a medida do arco AB é 5 vezes a medida do
arco u. Denotando a medida
do arco AB por m(AB) e a medida do arco u por m(u), temos
m(AB)=5 m(u).
Ø A
medida de um arco de circunferência é a mesma em qualquer um dos sentidos. A medida
algébrica de
um arco AB desta circunferência, é o comprimento deste arco, associado a um
sinal positivo se o sentido de A para B for anti-horário, e negativo se o
sentido for horário.
Unidade
de medida de arcos
A unidade de medida
de arco no SI é o radiano. Alem dessa, existem outras medidas muito utilizadas
por técnicos, que são grau e o grado. Sendo este último não muito comum.
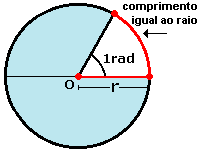
Radiano: Medida de um arco que tem o mesmo comprimento
que o raio da circunferência na qual estamos medindo o arco. Assim o arco
tomado como unidade tem comprimento igual ao comprimento do raio ou 1 radiano,
que denotaremos por 1 rad.
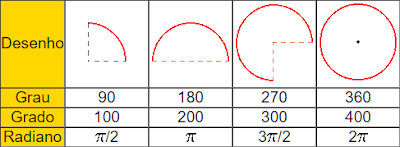
Grau: Medida de um arco que corresponde a 1º/360° do arco completo da circunferência na qual estamos medindo o arco.
Grado: É a medida de um arco igual a 1º/400º do arco completo da circunferência na qual estamos medindo o arco.
Grau: Medida de um arco que corresponde a 1º/360° do arco completo da circunferência na qual estamos medindo o arco.
Grado: É a medida de um arco igual a 1º/400º do arco completo da circunferência na qual estamos medindo o arco.
EXEMPLOS
PROBLEMA 1: O ponteiro maior de um relógio mede aproximadamente 1 m. Em quanto tempo a ponta móvel desse ponteiro percorre em 3π metros?
Solução:
O ponteiro do relógio é equivalente
ao raio da circunferência do próprio relógio. Então, a circunferência do
relógio mede:
Ccircunferência = 2πr
= 2 . 3,14 . 1 = 6, 28 m
Sabemos que o ponteiro maior do
relógio é o ponteiro dos minutos. Logo, ele dá uma volta completa na
circunferência em 60 minutos e essa volta completa corresponde ao comprimento
total da circunferência que é 6,28m. Assim:
60 min ---------- 6,28m
x min ---------- 3π m
Como 3π = 3 . 3,14 = 9,42m, temos:
60 min ---------6,28m
x min ----------9,42 m
Fazendo o produto dos meios igual ao
produto dos extremos, vem:
6,28 x = 60 . 9,42
6,28x = 565,2
x =
565,2/6,28
x = 90
minutos = 1 h 30 min.
PROBLEMA 2: (CESGRANRIO) Um mecanismo liga o
velocímetro (marcador de velocidade) a uma das rodas dianteiras de um
automóvel, de tal maneira que, quando essa roda gira 72π.rad ,
uma engrenagem que compõe o velocímetro gira 2π.rad .
Quando a roda gira 18π/5 rad,
essa engrenagem gira quantos graus?
Solução:
Aplicando a regra de três simples, temos:
 PROBLEMA 3: Determine em
radianos a medida do ângulo formado pelos ponteiros de um relógio às 4 horas.
PROBLEMA 3: Determine em
radianos a medida do ângulo formado pelos ponteiros de um relógio às 4 horas.
Solução:
Os ponteiros de um relógio estão ambos na direção
dos números somente na hora exata. Após esse momento, o único a ficar na
direção é o ponteiro dos minutos (grande). O relógio representa uma
circunferência dividida em 12 partes iguais. Logo, cada número dista de um arco
que mede 30º.
PROBLEMA 4: Determine.
Solução. O comprimento do arco “S” será
o produto da medida do ângulo central em radianos pelo raio.
a) o comprimento de um arco de circunferência (em
cm), sabendo que ela tem 12cm de raio e o ângulo central correspondente mede
20°.
a)
b) o ângulo central (em radianos) correspondente a
um arco de 15cm de comprimento, sabendo que ela tem raio de 20cm.
b)
c) a medida do raio de uma circunferência (em cm),
sabendo que nela um ângulo central de 15° corresponde a um arco de 30cm.
c)
APLICAÇÕES
A Trigonometria é um ramo da matemática
que trata das relações entre os lados e ângulos de triângulos (polígonos com
três lados). A trigonometria plana lida com figuras geométricas pertencentes a
um único plano, e a trigonometria esférica trata dos triângulos que são uma
seção da superfície de uma esfera.
A trigonometria começa como uma
matemática eminentemente prática para determinar distâncias que não podiam ser
medidas diretamente. Serve à navegação, à agrimensura e à astronomia. Ao lidar
com a determinação de pontos e distâncias em três dimensões, a trigonometria
esférica amplia sua aplicação à física, à química e a quase todos os ramos da
engenharia, em especial no estudo de fenômenos periódicos, como a vibração do
som e o fluxo de corrente alternada.
Astrônomo
Desde
a Antiguidade, os astrônomos estudam o movimento dos astros por meio de
ângulos, ou mais precisamente, por meio da trigonometria. Esse conhecimento é
muito usado para descrever os movimentos da Terra no espaço. Grande parte das
teorias matemáticas que descrevem o movimento dos astros, sejam eles planetas,
satélites, ou mesmo galáxias, exige um grande conhecimento de trigonometria.
Por
exemplo, no caso da chamada astronomia esférica, ou astronomia de posição, são
as direções nas quais os astros são vistos e as posições que ocupam sobre a
esfera celeste, medidas unicamente em ângulos, que importam para determinar a
posição de um astro.
Há séculos, a trigonometria
contribuiu, muito também para a descrição das posições dos objetos na
superfície da Terra, graças aos cálculos de longitude e latitude, medidas em
graus. Atualmente, utilizando modernos aparelhos de GPS, podemos localizar
pessoas e objetos, em qualquer ponto do planeta, com precisão de metros.
CURIOSIDADES
Os arcos trigonométricos
Os arcos trigonométricos
A Trigonometria, como outros
ramos da Matemática, não foi obra de um só homem ou nação. [...] Deve-se
lembrar que desde a época de Hiparco [século II a.C.] até os tempos modernos
não havia coisas como razões trigonométricas. Os gregos, e depois deles os
hindus e os árabes, usaram linhas trigonométricas. Essas a princípio tiveram a
forma de cordas num círculo, [...] e coube a Ptolomeu [século II d.C.] associar
valores numéricos (ou aproximações) às cordas. Para isso, duas convenções eram
necessárias: algum esquema para subdividir a circunferência de um círculo e
alguma regra para subdividir o diâmetro. A divisão de uma
circunferência em 360 graus parece ter estado em uso na Grécia desde os dias de
Hiparco, embora não se saiba bem como a convenção surgiu. Não é improvável que
a medida de 360 graus tenha sido tomada da astronomia, onde o zodíaco fora
dividido em doze “signos” ou 36 “decanatos”. Um ciclo de estações, de
aproximadamente 360 dias, podia facilmente ser posto em correspondência com o
sistema de signos zodiacais e decanatos, subdividindo cada signo em trinta
partes e cada decanato em dez partes. Nosso sistema comum de medida de ângulos
pode derivar dessa correspondência. Além disso, como o sistema babilônico
posicional para frações era evidentemente superior às frações unitárias
egípcias e às frações comuns gregas, era natural que Ptolomeu subdividisse seus
graus em sessenta partes minutae primae,
cada uma das quais era dividida em sessenta partes minutae secundae, e assim por diante. É das frases latinas que os
tradutores usaram que provêm nossas palavras “minutos” e “segundos”. Sem
dúvida, foi o sistema sexagesimal que levou Ptolomeu a subdividir o diâmetro de
seu círculo trigonométrico em 120 partes; cada uma dessas ele subdividiu de
novo em sessenta minutos e cada minuto de comprimento em sessenta segundos.
Sistema de Posicionamento Global (GPS)
O GPS (Global Positioning
System) ou Sistema de Posicionamento Global foi desenvolvido pelo Departamento
de Defesa norte-americano e destina-se a determinar a posição de um ponto na
superfície da Terra. Para isso, é utilizado um aparelho receptor de sinais de
rádio emitidos por satélites em orbita do planeta, que calcula as coordenadas
da posição do ponto.
As coordenadas de um ponto
sobre a Terra são dadas a partir de três referencias: o equador, a partir do
qual se determina a latitude; o meridiano de Greenwich, a partir do qual se
determina a longitude; e o nível do mar, em relação ao qual se estabelece a
altitude do ponto. Assim, para localizar um ponto sobre a Terra, como, por
exemplo, uma embarcação no mar, um avião, um caminhão de carga ou mesmo um
aeroporto ou um acidente geográfico, basta saber a latitude, a longitude e a
altitude em que se encontram.
O GPS baseia-se numa rede
estações terrestres que continuamente transmitem dados posicionais por meio de
sinais de rádio para um conjunto de 24 satélites artificiais, que dão duas
voltas completas em torno da Terra por dia, a uma altitude de 500 km. As
órbitas dos satélites foram escolhidas de modo que, de qualquer ponto da Terra,
possam ser observados pelo menos 4 deles.
Os satélites, por sua vez,
processam as informações recebidas das estações terrestres e, continuamente,
retransmitem sinais de rádio, que são captados e processados pelo receptor de
GPS, que dispõe de uma unidade de processamento capaz de decodificar em tempo
real a informação enviada por cada satélite e calcular a posição. Cada satélite
envia sinais de características diferentes em intervalos de 30 em 30 segundos e
de 6 em 6 segundos. Uma determinação precisa de posição requer uma boa recepção
dos vários tipos de sinais enviados.
O GPS utiliza técnicas de
triangulação e cálculos trigonométricos que se assemelham muito aos mais
tradicionais processos de localização, baseados em instrumentos convencionais
com referenciais astronômicos, usados, por exemplo, por Cristóvão Colombo e
outros grandes navegadores. Os grandes diferenciais são, sem dúvida, o controle
da posição dos satélites, a transmissão de sinais de rádio e o processamento
computadorizado do receptor.
Pra fins civis, o GPS
fornece um grau de precisão de 100 m para latitude e longitude. Se
considerarmos que 1 grau de latitude corresponde a um arco de aproximadamente
110 km, podemos dizer que o GPS fornece posições na superfície da Terra com
precisão de décimos de milésimo, ou seja, 1 em 10.000. Já para fins militares e
científicos, existem modos de operação do GPS que fornecem posições com
precisão de 22 m para latitude e longitude. Isso significa que sistemas de
segurança, como o de controle aéreo do SIVAM, na região amazônica, operam com
uma precisão de centésimos de milésimo, graças à tecnologia do GPS.
Engenheiro
aeronáutico
Quem
se forma em Engenharia aeronáutica sai da faculdade com conhecimentos
fundamentais para a elaboração de projetos de aeronaves – aviões comerciais,
jatos supersônicos, helicópteros e até mesmo foguetes. Como nas demais
engenharias, a Matemática é ferramenta essencial.
Para
desenhar peças tridimensionais do motor ou da fuselagem de um avião, o engenheiro
tem de entender de projeções. Para calcular a inclinação correta que as asas de
uma aeronave devem ter para decolar e aterrissar de maneira segura, são
necessários conhecimentos de trigonometria aliada aos modelos matemáticos que
descrevem a sustentação de um avião no ar.
Além
de participar da construção e da manutenção de peças mecânicas ou equipamentos
eletrônicos na indústria aeronáutica, esse profissional tem também a
alternativa de se especializar em tráfego aéreo. Seja na área que for, a Matemática
faz parte constante de sua vida profissional.
Referências Bibliográficas
http://www.matematicamania.com.br/2015/circunferencia-trigonometrica-resumo/
http://pessoal.sercomtel.com.br/matematica/trigonom/trigo01.htm
http://cadernodigital102.blogspot.com.br/2011/02/razoes-trigonometricas-na.html
Fonte: professorwaltertadeu.mat.br/GABTrigonArcosangulos2010.doc
http://www.coladaweb.com/matematica/funcoes-trigonometricas
Fonte: YOUSSEF, Antonio Nicolau;
FERNANDEZ, Vicente Paz; SOARES, Elizabeth. Matemática: Ensino Médio, vol.
único. São Paulo: Scipione, 2011.
Fonte: BOYER, Carl. História
da Matemática. Trad. Elza F. Gomide. São Paulo: Edgard Blucher, 1994. p.
116 e 121.
Engenheiro
aeronáutico
http://www.matematicamania.com.br/2015/circunferencia-trigonometrica-resumo/
http://pessoal.sercomtel.com.br/matematica/trigonom/trigo01.htm
http://cadernodigital102.blogspot.com.br/2011/02/razoes-trigonometricas-na.html
Fonte: professorwaltertadeu.mat.br/GABTrigonArcosangulos2010.doc
http://www.coladaweb.com/matematica/funcoes-trigonometricas
Fonte: YOUSSEF, Antonio Nicolau;
FERNANDEZ, Vicente Paz; SOARES, Elizabeth. Matemática: Ensino Médio, vol.
único. São Paulo: Scipione, 2011.
Fonte: BOYER, Carl. História
da Matemática. Trad. Elza F. Gomide. São Paulo: Edgard Blucher, 1994. p.
116 e 121.






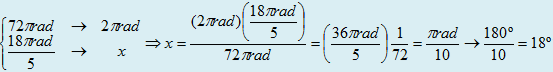
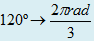







0 comentários: